 Dr No is hopeless with numbers. Just being in the presence of statisticians causes a pressure of incomprehension to build up in his head. When they start to talk numbers, it is as if they are speaking in tongues; and when their chalk squeaks on the blackboard, all he sees is so many hieroglyphics.
Dr No is hopeless with numbers. Just being in the presence of statisticians causes a pressure of incomprehension to build up in his head. When they start to talk numbers, it is as if they are speaking in tongues; and when their chalk squeaks on the blackboard, all he sees is so many hieroglyphics.
But numbers are part of the fabric of medicine, and their understanding is necessary to the practice of medicine; and so Dr No has over the years developed a habit of translating the hieroglyphics into words, and the formulae into verbal instructions. Σx becomes the sum total of all the values of x; and μ = Σx/n becomes find the average value of x by adding them together, and dividing by the number in the sample. The dark impenetrable pool of numeracy is side-stepped on the well-worn plank of words.
And so it is that Dr No has been able to make at least partial sense of the many numbers that are bandied about in the medical world. One such number, much in the news these days as a way of comparing numbers of hospital deaths, is the SMR, or Standardised Mortality Ratio.
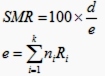 A standard statistical text might inform us that the SMR is simply calculated by using the formula shown on the right. This, whilst no doubt makes good sense to statisticians, it is of no use to man nor beast. So let us tackle the problem in a manner more amenable to understanding – by the use of words.
A standard statistical text might inform us that the SMR is simply calculated by using the formula shown on the right. This, whilst no doubt makes good sense to statisticians, it is of no use to man nor beast. So let us tackle the problem in a manner more amenable to understanding – by the use of words.
Let us say our local hospital, St Swithin’s, has two hundred deaths a year, while neighbouring St Clement’s has but a hundred. On the face of it, as patients, we stand a better chance if we go to St Clement’s; but, of course, it isn’t as simple as that.
What if St Swithin’s was twice the size of St Clement’s, and treated twice as many patients? Then we might expect twice as many deaths: and so, to give a better comparison between the two, we might prefer to use not the absolute numbers, but rates of death per number of patients; and if St Swithin’s was indeed twice the size, then we might find that the rates of death were similar – each having, let say, ten deaths a year per thousand patients; but because St Swithin’s treats twenty thousand patients a year to St Clement’s ten thousand, St Swithin’s clocks up two hundred deaths to St Clement’s one hundred, while the actual risk of death remains the same in each.
But, let us say, the two hospitals treat the same number of patients, and so St Swithin’s death rate is indeed twice that of St Clement’s. Once again, St Clement’s appears the better hospital – but of course, it isn’t as simple as that.
What if St Swithin’s is in an area of retirement homes, while St Clement’s caters to a young and affluent population? Both have the same number of admissions, but those admitted to St Swithin’s are old and frail, while those admitted to St Clements are young and fit. Since the old and frail are more likely to die, we would expect more to die in St Swithin’s than St Clement’s; and so we would expect a higher death rate, because we are not comparing like with like. The trouble is – St Swithin’s might still be a bad bet, even though it admits old frail patients that might appear to explain the high death rate – but don’t.
So we might chose to look more closely at the death rates, perhaps dividing (stratifying in the jargon) them into age bands. We would then be comparing like with like (so far as age is concerned), and would be able to see, after scrutinising the figures, how the two compared.
Stratified rates are indeed a valid way to compare rates, but they involve many comparisons; and once more factors – say sex, affluence, pre-existing illness, whatever – are brought to bear, the number of comparisons begins to rise exponentially, and rapidly becomes not only unwieldy, but verging on the futile, as each individual row in each table ends up with smaller and smaller numbers such that we loose perspective.
This is where the SMR comes to our aid. What if we had age/sex/whatever specific death rates for a large population – let us say the whole country – then we could, knowing the number of patients in each age/sex/whatever band for each hospital, work out the expected number of deaths at each hospital assuming it had the national death rate for each band.
We could then compare the actual (observed) number of deaths with those we would have expected, had our hospital had the same age/sex/whatever death rate pattern as our large, reference population, for example by dividing the observed number by the expected number, to get a ratio. If the numbers were the same, the ratio would be one (1.00); if there were more deaths than expected, the ratio would be greater than one; less deaths than expected would cause the ratio to be less than one.
Conventionally, this ratio – the SMR, or Standardised Mortality Ratio – is multiplied by 100, such that an SMR of 100 means observed deaths match the expected number; over 100 means more deaths than expected, and less than 100 means less deaths than expected. We now have, in a single summary figure, a number that expresses how our hospital does, compared to what might be expected had our hospital the same rates as the rest of the country.
So far, so good. This method – which is known as indirect standardisation – is indeed the method used to calculate the H(ospital)SMRs that are so in evidence in the news at present. But there are prices to be paid for achieving a convenient single summary figure. Firstly, by drawing back, so to speak, to see that single figure, we can loose sight of important detail – the single figure has the effect of masking quite possibly vital information that is contained in the detailed figures. And secondly, and perhaps more importantly, given the current furore over HSMRs, an HSMR can only tell us how our hospital compares to the big picture (that is, the national picture, or whatever reference population we used), at a given point in time. Directly comparing HSMRs from two hospitals – St Swithin’s and St Clement’s, or even between different years at the same hospital, can be prone to significant error, for a variety of reasons.
And there’s the rub. We still don’t really know whether St Swithin’s is killing more patients than St Clement’s because it is a rogue hospital, or because it is the victim of a valid mitigating factor. All the furore is based, once again, on what may well be dodgy stats.
Once Dr No’s head has cleared, and if he is feeling benevolent, he might, just might, write a post that explains why they are dodgy.
